機械学習モデルの評価ポイントについて

投稿日：2021年1月15日

作成した機械学習モデルを評価する際には、単純な正解率や精度のみを観察せずに、
各々の課題に即した適切な評価を行うことがとても重要です。
そのための道具の中でも代表的なものに、二値分類（※1）で用いられる
混同行列（※2）と呼ばれるものがあります。

分かりやすいように、ここでは『医療機器で測定したデータから、患者が将来難病を患いそうか否か』を
識別する機械学習モデルを作ったとしましょう。
学習データには、実際に難病を患った人とそうはなっていない人の
過去の測定データを5000件用いたとします。

混同行列の値を用いた基本的な指標で実際に機械学習モデルを評価した結果、
例えば以下の様な結果になったとします。
TP 500 / TN 4150 / FP 450 / FN 500
Accuracy 0.93 / Precision 0.526315789473684 / Recall 0.5
F-measure 0.512820512820513

上記の『TP、TN、FP、FN』はそれぞれ以下の意味を持ちます。
（『Accuracy、Precision、Recall、F-measure』については後述）

• 真陽性(True Positive)
  病気になった人を病気になると判断した数。
• 真陰性(True Negative)
  病気にならなかった人を病気にならないと判断した数。
• 偽陽性(False Positive)
  病気にならなかった人を病気になると判断した数。
• 偽陰性(False Negative)
  病気になった人を病気にならないと判断した数。

こうした言葉を「新型コロナウイルスに関する報道で見かけたことがある！」という方も
多いのではないでしょうか。
細かい用語などには差異がありますが、実はこうした考え方は機械学習モデルの評価にも利用されています。

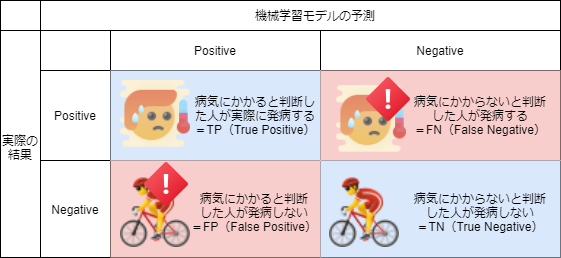
言葉だけでは分かりにくいと思いますので、以下の図も併せてご覧ください。
青背景が機械学習モデルが正しく判断出来た部分、赤背景が機械学習モデルが誤った判断をした部分
になります。

この4つを元に、以下の評価項目を算出することが出来ます。

• 正確度（Accuracy）
  全データの内、どれだけ判断が正解だったか
  計算式： (TP+TN) ÷ (TP+TN＋FP＋FN) 
• 適合度（Precision）
  陽性（≒病気になる）と判断されたデータの内、
  どれだけ判断が正解だったか　
  計算式：TP ÷ (TP+FP)
• 再現率（Recall）
  実際に陽性（≒発病した）と判断されたデータの内、
  どれだけ判断が正解だったか
  計算式：TP ÷ (TP + FN)

そして、それぞれの評価項目を今回の結果に当てはめてみると次の様な評価をすることが出来ます。

• 正確度(Accuracy)
  単純な正解率は93%という意味になり、この値だけ見ればよく出来たモデルに見えます。
• 適合率(Precision)
  この数値は52%程度しかなく、病気になる人を正確に判別することが出来ていないことが分かります。
  なぜなら、機械学習モデルが「この人は病気にかかってしまう」と判断した後、実際にそれが的中した
  （≒実際に病気を発症した人の）割合が50%程度しか無いという事だからです。
• 再現率(Recall)
  この数値も50%しかなく、半数の病気になる人を見逃していることが分かります。

ここから、この機械学習モデルの精度は高く見える一方で、視点を変えて再度評価してみると、
実は精度の低いモデルだったということが分かるのです。

ここで、この機械学習モデルの精度を高めるためには、適合率と再現率を両方高める必要があるのか
という疑問が出てくると思います。
結論から先に書いてしまいますと、適合率と再現率はトレードオフの関係になっており、
両方を追求することは出来ません。
そのため、評価に当たっては二つの値の調和平均（ 2 ÷ (1/Precision + 1/Recall) ）を取った
F値(F-measure)も算出することが普通です。

大事なのは適合率と再現率を天秤にかけ「どちらの評価がより優先度が高いか」の判断をしつつ、
「優先度が低いもう一方はどの程度の評価であれば許容できるか」をしっかりと考え、
関係者で擦り合わせていくことです。
例えば今回の場合は「将来的に病気を患う可能性が高い人に適切な注意喚起が出来る」方が望ましいことが
一般的で、再現率が高いモデルが望ましいと思われます。

～～～まとめ～～～

このテストデータの9割は「病気にならなかった人」のデータであり、
極論「絶対に病気にならないとしか答えないルール」でも90%の正解率を叩き出すことは出来てしまいます。
混同行列やそこから計算した指標を見る限り、出来上がっていた機械学習モデルはまさにそれに近い
「残念なモデル」であったことが分かります。

一般的に、病気の人は「その病気ではない人」に比べて圧倒的に数が少なく、このような分類先のデータ数がその性質上不均衡となるデータを用いて機械学習モデルを作成する時は細心の注意が必要です。

～～～参考文献～～～

• 平井 有三,はじめてのパターン認識, 森北出版株式会社, 2012

～～～注釈～～～

※1 二値分類
結果を二分出来る問題の事。
例えば男性と女性というように2つに分類するような分け方や
x >= 0.5 の場合合格とし、それ以下の場合は不合格にする等があたる。

※2 混同行列
二値分類問題で出力されたクラス分類の結果をまとめた行列の事で、
学習モデルの性能を測る指標として使用される。

---

powered by icons8